Made with 3Blue1Brown's animation engine: manim
The Problem
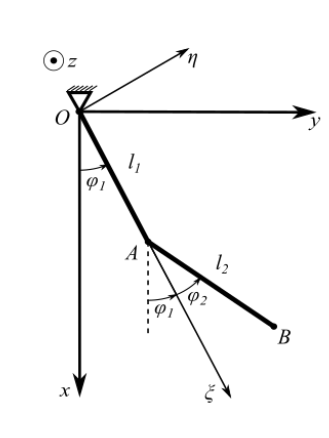
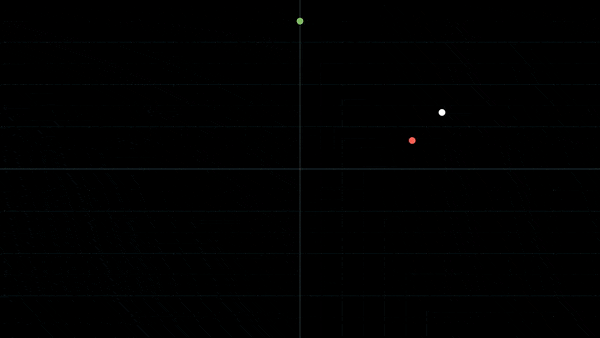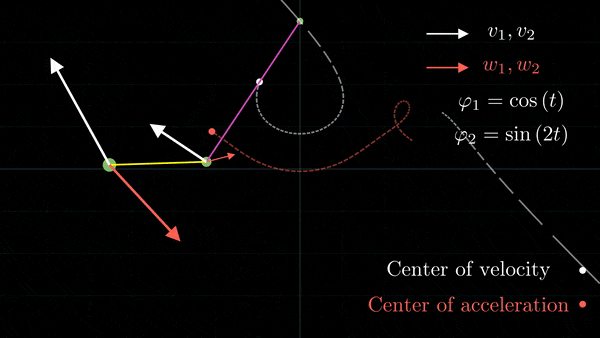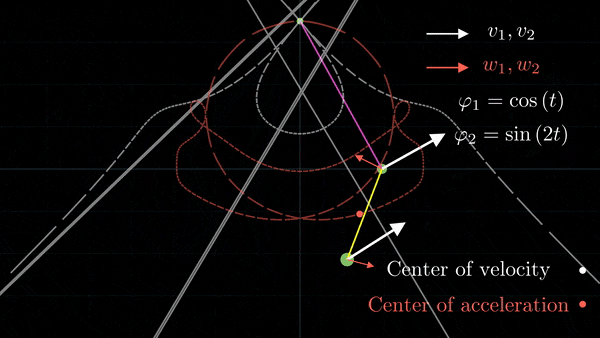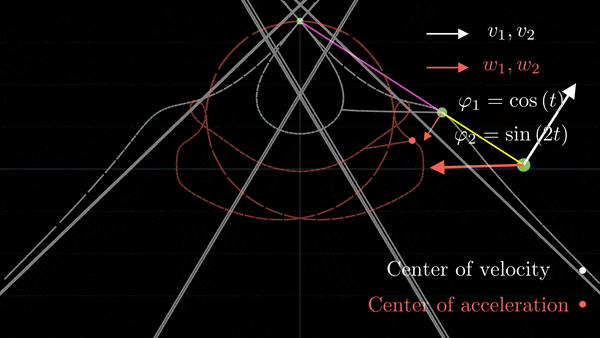
Given the angles φ₁ and φ₂ as functions of time, we show the positions of point A and B, and also the velocity and acceleration vectors at every point in time. Also, we draw the trajectories of the instantaneous centers of zero velocity and acceleration.
To do this, we use the python library SymPy to differentiate the position vectors of both points. This way, it's possible to input any two function that are twice differentiable.
SymPy also comes in handy to output our functions as LaTeX so we can show it on the demonstration.
How to run it
First you'll need to have manim installed. You can clone into the repository:
git clone https://github.com/3b1b/manim.git
cd manim
Then, in that directory run:
python3 -m pip install -r requirements.txt
Next, in that same directory, clone this repository (or simply copy the file 'double_pendulum.py') and execute:
git clone https://github.com/sofiabelen/Double-Pendulum.git
python3 manim.py double_pendulum.py DoublePendulum -pl -r 1080
Change '1080' to whatever resolution you want.