First of all, I want to say that I'm very grateful to Vasily Pisarev for his mentoring on this project! It's my first time writing a CFD solver from scratch and I've working on it since my second year at MIPT. It is sometimes a challenge finding the time and energy to work on this alongside the usual university workload, but it is also an important source of motivation for me. A big moment for me was when I presented it at the 64th International MIPT Scientific Conference. I am forever grateful to my department for giving me that opportunity. Check out my certificate of participation!

Motivation: Enhanced Oil Recovery Using Gas Injection

The motivation of our simulation is the technique called enhanced oil recovery. Our goal is to model the view from above of this process as a 2d problem.

For now, we assume that the components do not mix, but it is in our future perspective to model the balance of phases, or, in other words, a multiphase flow problem.

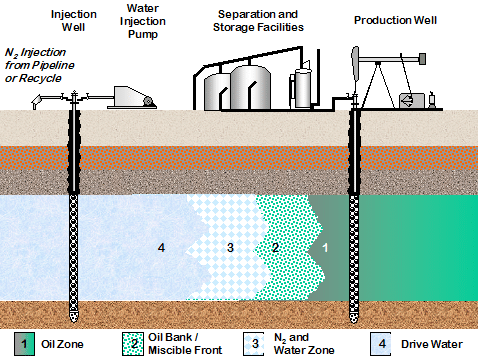large An Overview of Oil Production Stages: Enhanced Oil Recovery Techniques and Nitrogen Injection January 2015. International Journal of Environmental Science and Development 6(9):693-701 DOI:10.7763/IJESD.2015.V6.682

Flow Through a Porous Medium

The macroscopic flow equations are obtained by averaging the hydrodynamic equations on a volume, containing many pores.

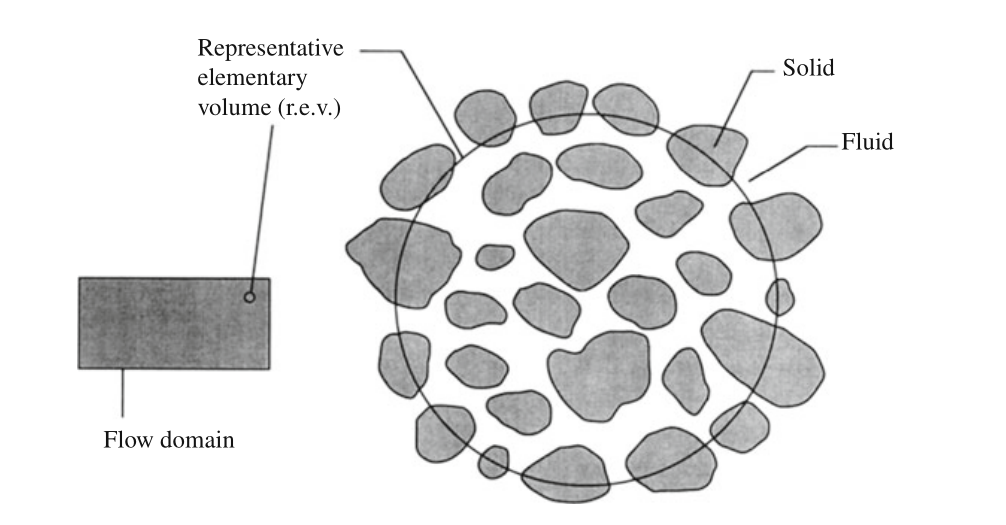large An Overview of Oil Production Stages: Enhanced Oil Recovery Techniques and Nitrogen Injection Convection in Porous Media. Authors: Donald A. Nield Adrian Bejan

The filtration velocity $\vec v$ is defined as the average fluid velocity over a volume containing both solid and fluid material.

$$ \vec v = \varphi \vec V_f $$ here $\varphi$ is the porosity, and $\vec V_f$ is the average fluid velocity over a volume consisting only of fluid material.

Continuity Equation of Each Component

$$ \varphi \frac{\partial \rho_i}{\partial t} + div (\rho_i \vec{v}_i) = 0 $$ where $\rho_i = \frac{m_i}{V}$.

Tait Equation to Relate Liquid Density to Pressure

$$\frac{\hat{\rho} - \rho_0}{\hat{\rho}} = C \log_{10} \frac{B + P}{B + P_0}$$ where $C = 0.2105$,

$\rho_0 = \frac{1}{67.28 \frac{m^3}{mol}}$,

$P_0 = 0.1 MPa$,

$B = 35MPa$, in the case of $C_5H_{12}$.

Ideal gas equation of state

$$P = \frac{RT}{M} \hat{\rho}$$

Darcy's Law

$$ \vec{v_i} = -\frac{1}{\mu_i} \hat K \cdot f_\alpha (s) \cdot \nabla P$$

$K$ - permeability coefficient,

$f_i(s)$ - relative phase permeability, which depends on the saturation (as an approximation we take $f_i(s_i) = s_i^2$),

small

$\mu$ - dynamic viscosity,

$s$ - saturation.

Initial and Boundary Conditions

small

Methods Used

  1. Second order finite difference method for spatial discretization using a staggered grid.

  2. Explicit predictor-corrector method according to the Heun scheme for time integration.

  3. Newton-Raphson method for finding pressure and gas saturation.

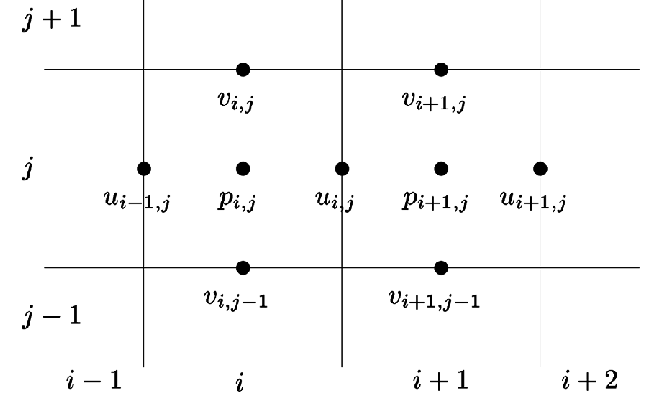small Staggered Grid.

Algorithm

  1. We are given the densities $\rho_i = \rho_i(t)$.

  2. Finding the pressure and gas saturation using the Newton-Raphson method from the condition of equality of the pressure of the gas and the liquid:

$$P = P_1 \left( \frac{\rho_1}{s} \right) = P_2 \left( \frac{\rho_2}{1 - s}\right)$$

  1. Calculation of fluxes from Darcy's law.

  2. Calculation of the densities $\rho_i(t + \Delta t)$ based on the known fluxes.

  3. Renaming $\rho_i = \rho_i(t + \Delta t)$ and moving on to the next time step.

Results

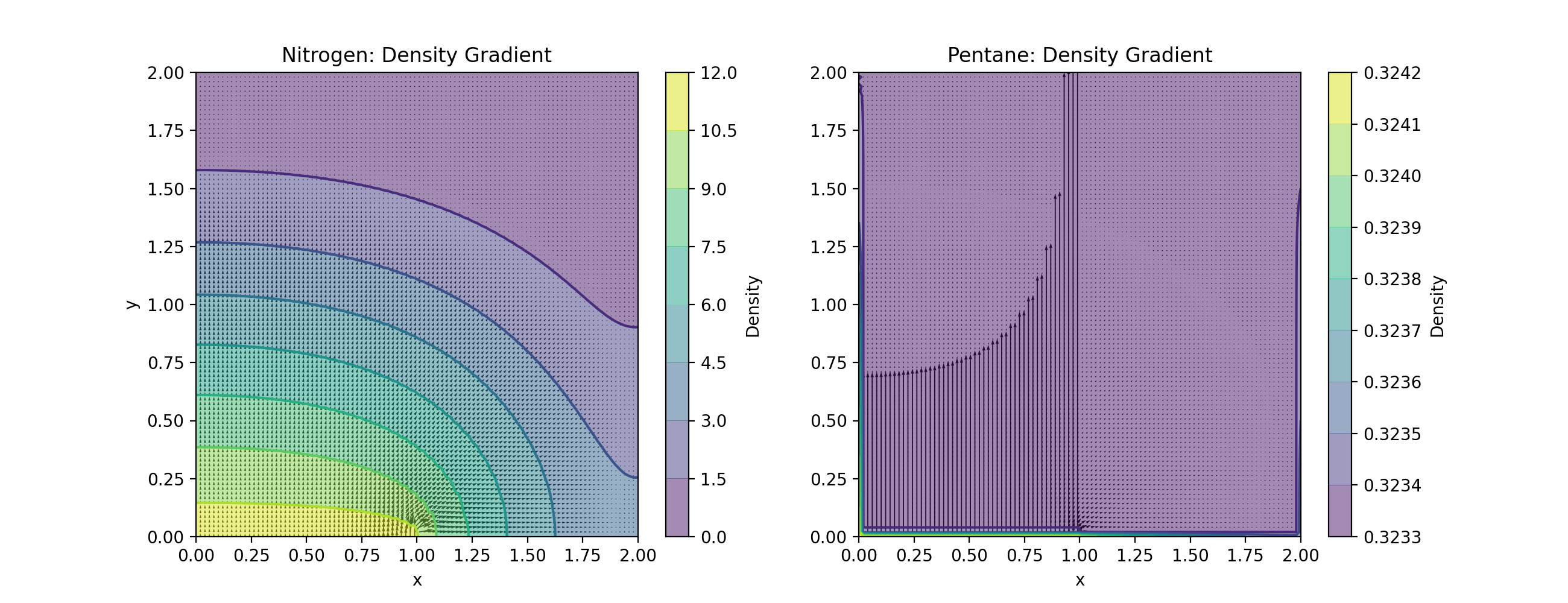
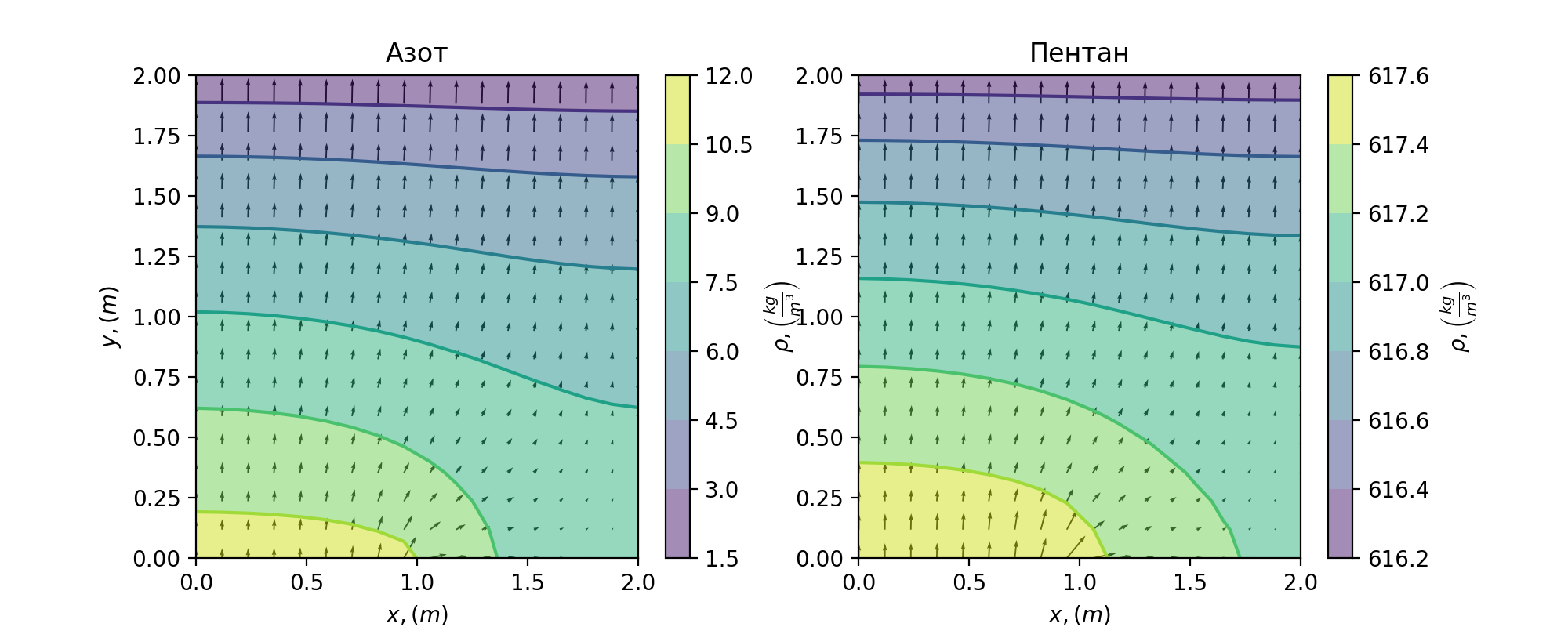huge Densities and Velocity field after 500s. The first image corresponds to Nitrogen and the second to Pentane.

huge

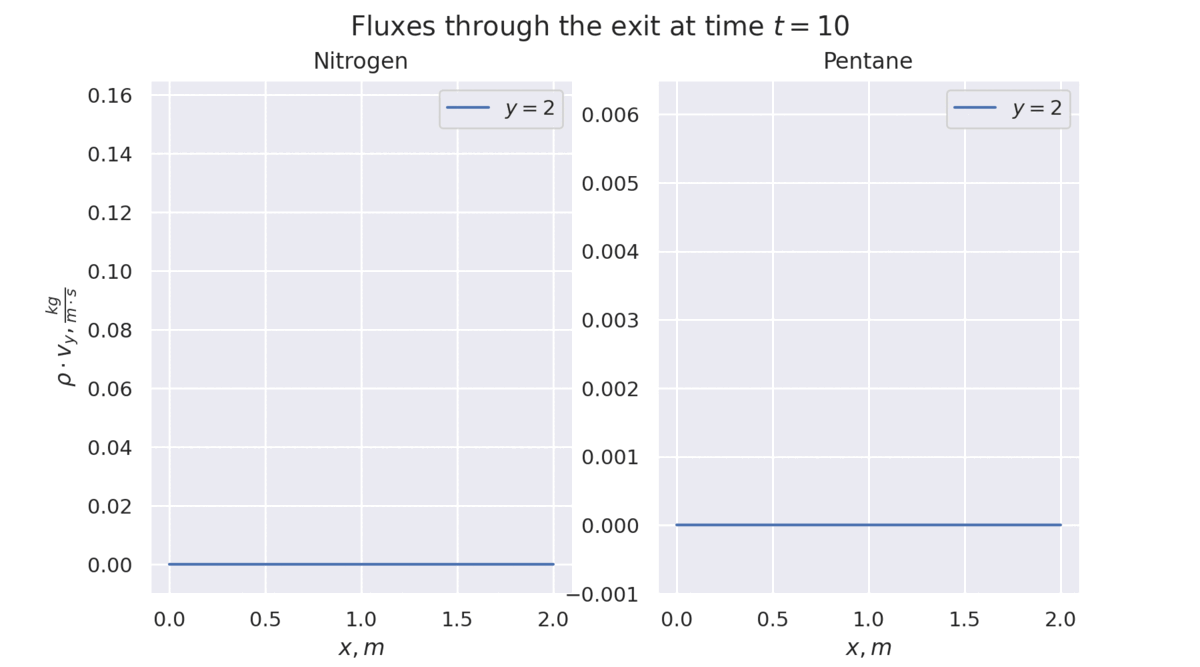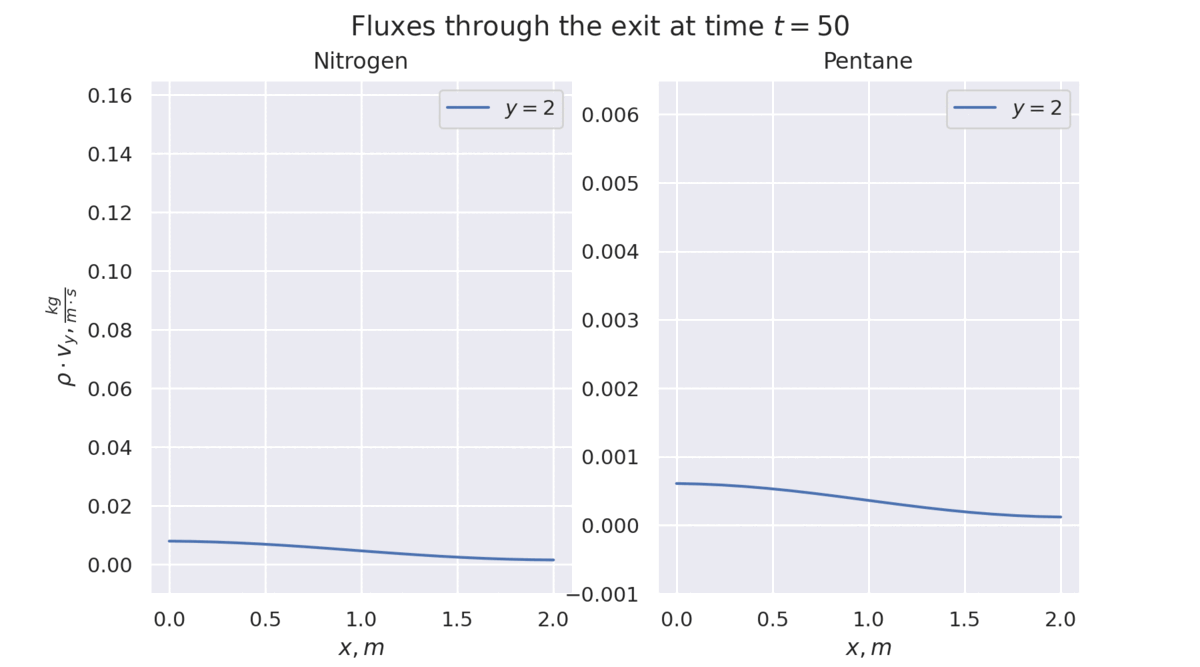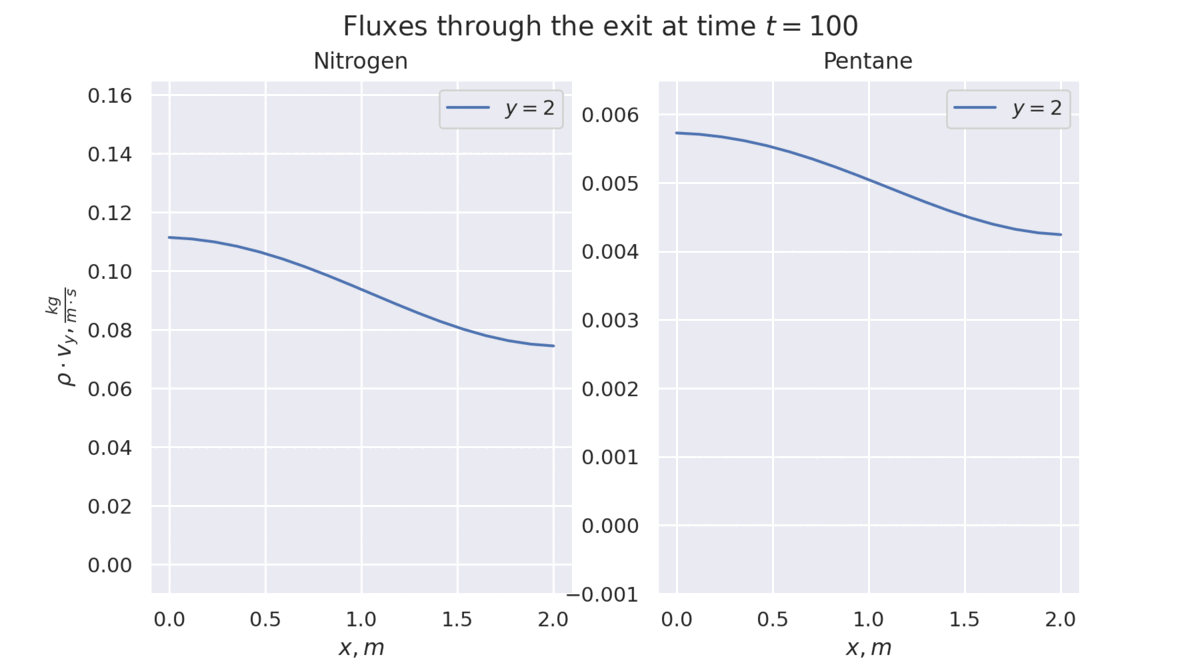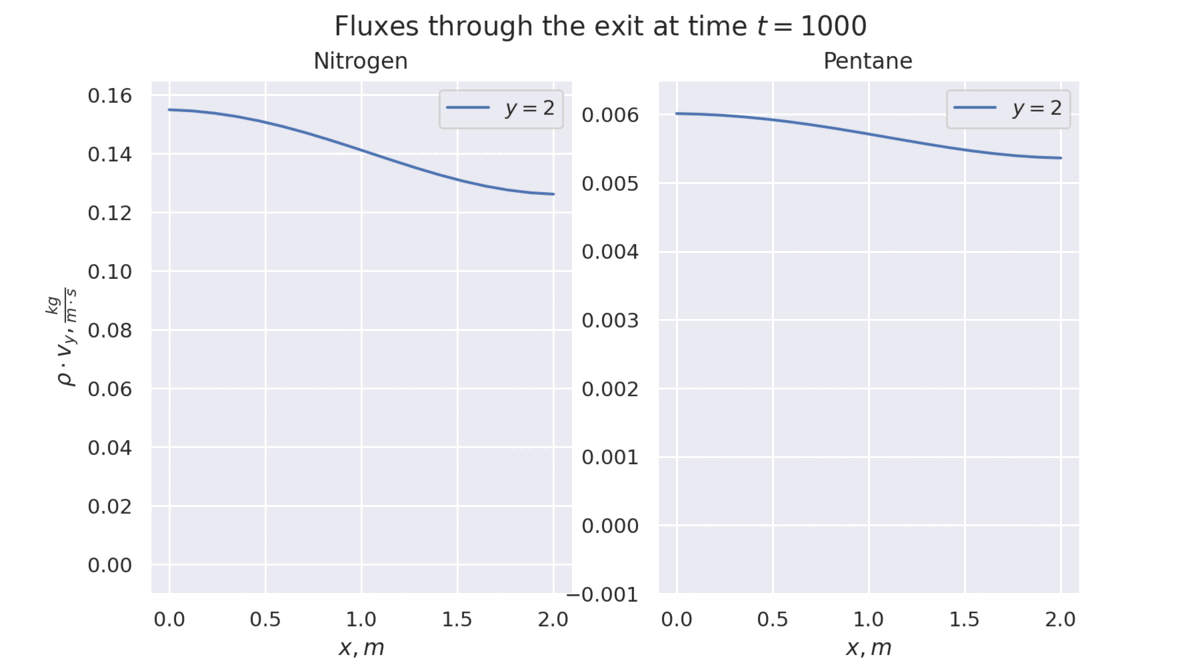
What I've Learned So Far

  • Basic notions about multiphase flow and filtration: how the flow of each component is inhibited by the presence of the other, how Darcy's law looks like when there is more than one component present.

  • Better understanding of how to work with boundary conditions: ghost cells, making sure they are the same order of complexity as the rest of the scheme.

  • Profiling and optimization. Type stability in Julia.

  • Organization of medium size project. Function overloading, functors, modules.

Troubles Faced

  • Oscillating error resulting from the central difference scheme.

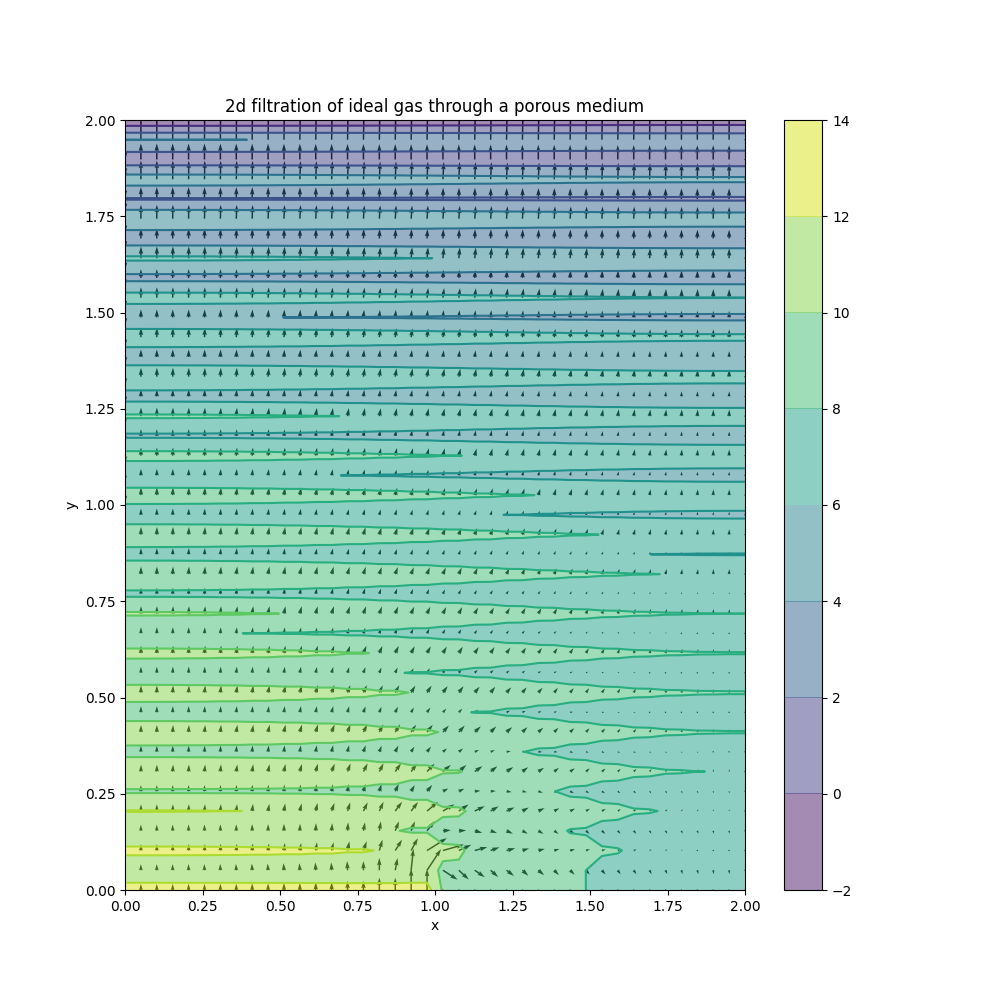
large

  • Changing the BC in the code was inconvenient, so we had to automatize the process by creating a structure that holds the BC and the use of bit masks.

  • The sharp step from $P_{in}$ on the inlet to $P_0$ on the inside was causing problems, so we had to increment $P_{inlet}(t)$ linearly with time from $P_0$ to $P_{in}$.

huge

  • Switched to upwind scheme to ensure the conservation of mass.

What I Would Do Better Next Time

  • Start writing documentation from the start :)

  • Write code in a more modular style from beginning.

Check out the source code!